变量与数据类型

在C语言语法中，变量代表保存数据的存储单元，在定义变量时，应指定变量名和数据类型，如：

int number, i;

float x;

double area, length;

通过定义一个变量，代表在内存中指定一个存储单元，用以存放该变量的值，而该存储单元的大小由变量的数据类型决定。

数据在内存中是如何存储的？

整型数据

以short int 为例，整型数在内存中用2个字节存储(16位二进制），其中最高位为符号位，0表示正数，1表示负数。

如：0 000 0000 1000 0001 表示正的十进制数：2⁷+2⁰=+129

计算机数值的表示方法包括原码、反码和补码，内存中数据保存采用补码，正数的原码、反码和补码是一样的，而负数则不同。

-1的表示如下：

• 原码 1 000 0000 0000 0001 符号位为1，其余位为1的二进制表示。

• 反码 1 111 1111 1111 1110 原码取反（符号位保持不变）

• 补码 1 111 1111 1111 1111 反码＋1

可知： 1 111 1111 1111 1111 即为内存中 -1 的二进制形式。

16位二进制能表示的最大值和最小值分别为：（补码）

0 111 1111 1111 1111 =2¹⁵-1 = 32767

1 000 0000 0000 0000 = -2¹⁵ =-32768

由此可知，不同类型的整型数据能表示的数值范围不同，以下是目前流行的32位编译器的各种整数类型表示范围：

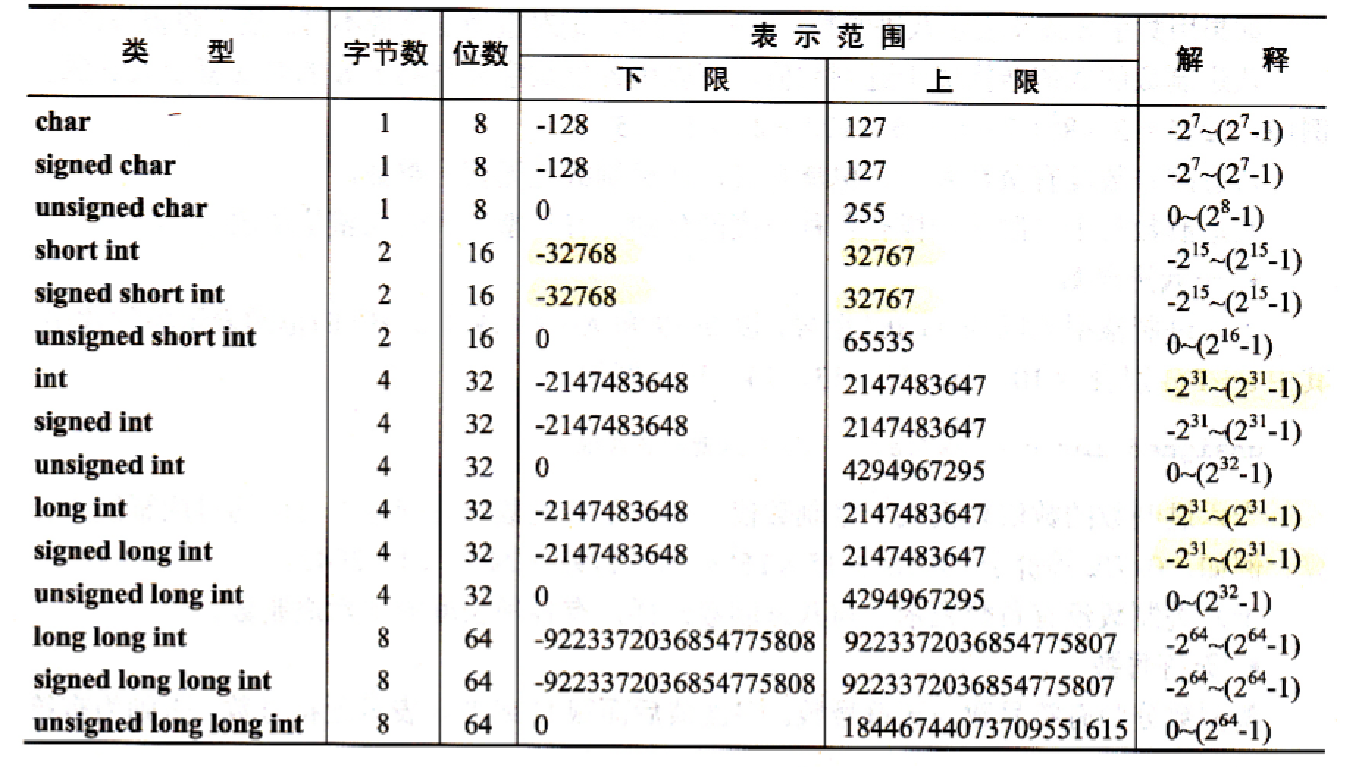
可以这样理解：对于16位的short int型数据，仅能保存从-32768到32767之间的数值，存储超过此范围的数据将造成整型数的溢出。

浮点型数据

浮点型数据包括单精度浮点型 float和双精度浮点型 double，float用4字节存储，double用8字节存储。

以单精度浮点型为例，float是用32位二进制存储，包括1位符号位、8位阶码、23位尾码。

如实数 26.0的浮点数存储表示如下： （引自中国大学MOOC平台课程计算概论与程序设计基础（北大李戈））之 “C 语言中的数据成分”）

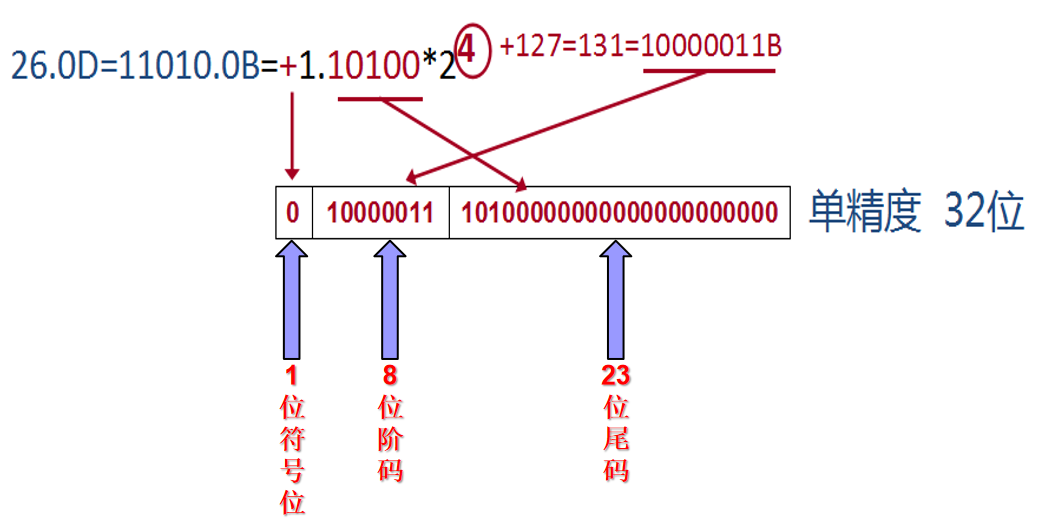
即：

• 取值范围：8位阶码（二进制）能表示的十进制数为38位。

• 数据精度：1.XXX的固定表示和23位尾码能精确表示的十进制数约为7位。

可以这样理解：对于单精度浮点型数据，虽然可以存储38位十进制的实数，但仅前7位数是精确无误的。

整型溢出问题

由于各类型整型数据能表示的范围有一定的限制，当数据超出该类型的存储范围时，会造成整型数的溢出。

如short int 型的最大值为32767，二进制表示为：0 111 1111 1111 1111

当该数+1后将变为：1 000 0000 0000 000 即：-32768

显然，该整型数的计算超出了short int型的存储范围，造成整型数的溢出。

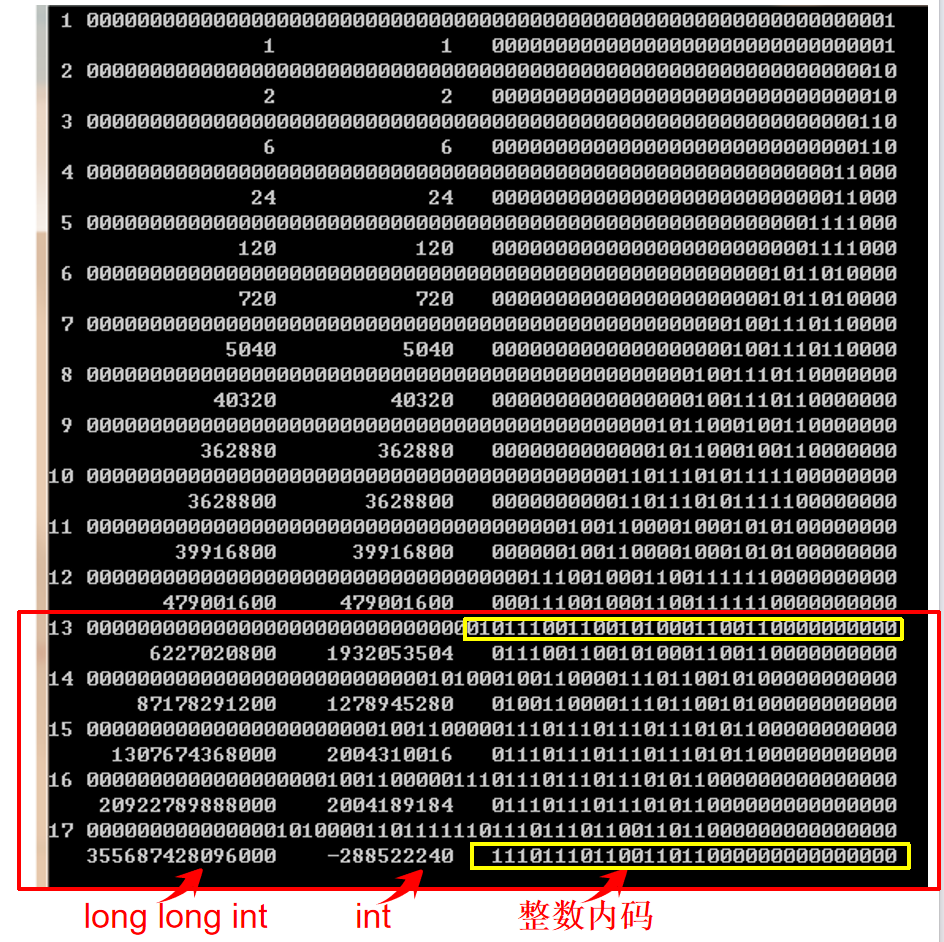
如下求阶乘的程序段中，求17！时出现了负数，显然是由整型数的溢出造成。

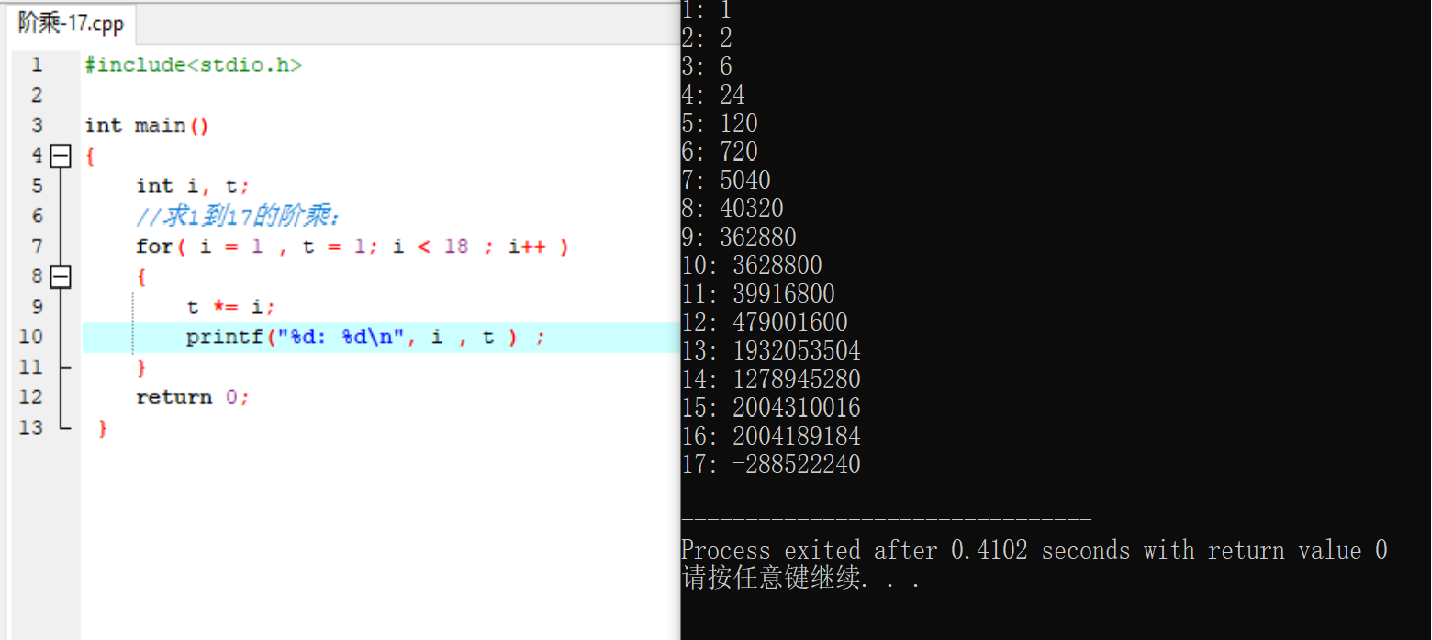
当定义变量 t 为 long long int 型（64位）时，17！的值仍在 long long int型的表示范围内，未出现溢出。

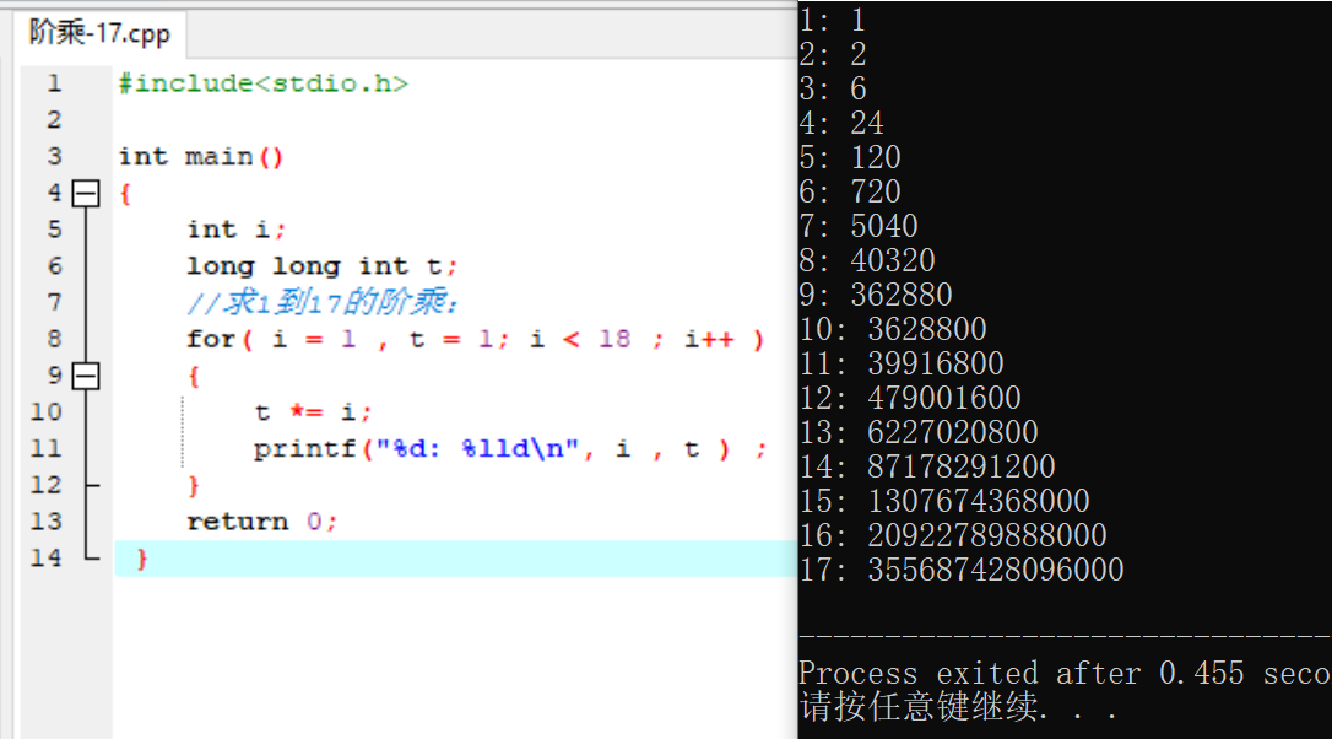
通过在求阶乘过程中打印整数的二进制码形式，发现当计算13！时就已经超出了int型（32位），实际上已经出现整型溢出问题。仅当计算17！时的最高位32位出现1时，显示出负数形式。

浮点数的精度问题

由于浮点数存储方式不同于整型数，得出一个结论：并不是所有的实数都能在计算机中精确表示。

如下程序段对浮点数进行如下定义和赋值：

#include<stdio.h>
int main()
{
	float x=3.141592653589793238462643383279;
	float y=1.2e38;  
	float z=1.2e50;
	printf("x=%.10f\ny=%f\nz=%f\n",x,y,z);
	return 0;	
 } 

输出结果如下：

由于浮点数的精度问题，对于一个浮点型变量的赋值与实际存储在内存中的数值可能并不相同，由此可见，虽然float型可以存储38位十进制的实数，但仅前7位数是精确无误的。

针对浮点数可能出现的精度问题，在编写程序时，在对浮点数进行等值比较时，经常会出现失效的情况。如下示例：

#include<stdio.h>
#include<stdlib.h>

int main()
{
	double x=12345678.9*9;
	double y=111111110.1;  //x的计算结果 
	if(x==y)
		printf("same\n");
	else
		printf("not same\n") ;
	printf("x=%.10f\ny=%.10f\n",x,y);
	return 0;	
 } 

输出结果如下：

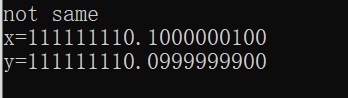
因此，在对浮点数进行等值比较时，不能将两个浮点数直接进行比较，而是通过比较两个浮点数的绝对误差是否小于一个给定的精度值如1e-6，如果小于则判定这两个浮点数相等。

#include<stdio.h>
#include<math.h>

int main()
{
	double x=12345678.9*9;
	double y=111111110.1;  //x的计算结果 
	if(fabs(x-y)<1e-6)
		printf("same\n");
	else
		printf("not same\n") ;
	printf("x=%.10f\ny=%.10f\n",x,y);
	return 0;	
 } 

输出结果如下：

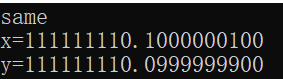
本篇更多相关内容请参看集美大学学校云SPOC课程 "高级语言程序设计" 之 ”第五周 循环控制“--”4 回顾数据类型与表达式“